[운영체제] Memory Management 4 (불연속할당/Paging 기법)
연속 할당 : 프로그램이 메모리에 올라갈 때 통째로 메모리에 올라가는 방식 불연속 할당 : 프로그램을 구성하는 주소 공간을 같은 크기의 페이지 단위로 잘게 쪼개서 페이지 단위로 메모리에
rannnneey.tistory.com
[ Two-Level Page Table (2단계 페이지 테이블) ]
두 단계 페이지 테이블은 공간을 줄이기 위해서 사용한다.
2단계 페이지 테이블은 페이지 테이블이 안쪽 페이지 테이블과 바깥쪽 페이지 테이블 두 개가 존재한다.
CPU가 논리적 주소를 주게 되면 페이지 테이블은 두 단계를 거쳐서 주소 변환을 하고 그다음 실제 메모리에 접근한다.
현대 컴퓨터 시스템은 각 프로그램에 메모리 크기랑 실제 물리적 메모리 크기와는 독립적이다.
물론 물리적 메모리가 크면 가능한 많은 내용이 물리적 메모리에 올라가기 때문에 더 빠르다.
그런데 어차피 페이지 단위로 나뉘어서 메모리에 올라오기 때문에 논리적 메모리가 물리적 메모리보다 크다고 하더라도 실행하는 데 문제는 없다.
현대 컴퓨터에서는 메모리 주소 체계가 굉장히 크다. 32bit의 Address를 사용하고 최근에는 64bit Address 체계를 사용한다.
논리적 주소는 프로그램마다 독자적으로 갖고 있는 주소 공간이며 메모리를 표시하는 주소 체계를 몇 bit를 쓰느냐에 따라 다르다.
32bit로 표현 가능한 전체 byte 정보는 232가지이다. 즉 메모리 주소가 0번지부터 231번지까지 주소를 매길 수 있다.
32bit 주소 체계는 4G를 표시할 수 있는데 4GB로 표시할 수 있는 총공간을 페이지 단위로 쪼갠다.
각각의 페이지 크기는 4KB이며 페이지의 총 개수는 1M 개다. 1M 개의 페이지 테이블 Entry가 필요하다는 뜻이다.
페이지 테이블도 메모리에 들어가야 되고, 각 프로그램마다 따로 존재하는 페이지 테이블을 메모리에 다 집어넣으면 공간낭비가 심해진다.
각각의 페이지 테이블 엔트리 하나의 크기가 4Byte, Entry의 개수가 1M 개이므로 각 프로세스마다 페이지 테이블을 위해서 4MB의 공간을 할당하여 공간 낭비가 심해진다. 그래서 2단계 페이지 테이블을 사용하겠다는 것이다.
여기서 한 가지 알아야 할 점은 전체 메모리 주소 공간 중에서 실제 프로그램이 사용하는 공간은 지극히 일부분이다.
프로그램의 주소 공간은 Code, Data, Stack으로 구성되어 있고 그 중간에는 사용되지 않는 논리주소가 상당 부분을 차지하고 있다.
페이지 테이블은 주소 공간 중간에 구멍이 있다고 해서 그 Entry를 빼고 만들 수 없다.
배열은 인덱스를 통해서 접근하는데 중간이 비어있으면 안 된다.
그러다 보니 결국 주소 체계 중에서 상당히 일부분만 사용됨에도 페이지 테이블 Entry는 다 만들어져야 한다.
✓ 현대의 컴퓨터는 Address Space가 매우 큰 프로그램 지원
✓ 32 Bit Address 사용 시 232(4GB)의 주소공간
✓ Page Size가 4K 시 1M 개의 Page Table Entry 필요, 각 Page Entry가 4B시 프로세스 당 4M의 Page Table 필요
그러나 대부분의 프로그램은 4G의 주소 공간 중 지극히 일부분만 사용하므로 Page Table 공간이 심하게 낭비됨
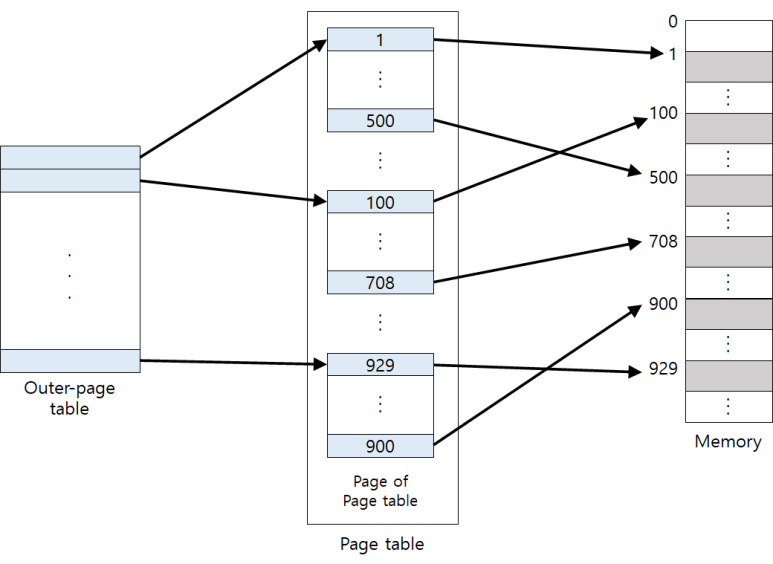
→ Page Table 자체를 Page로 구성, 사용되지 않는 주소 공간에 대한 Outer Page Table의 Entry 값은 NULL (대응하는 Inner Page Table이 없음)
● Two-Level Paging Example
페이지 내에서 Offset은 원래 존재했고 페이지 number가 세분화가 되었다.
바깥쪽 페이지 테이블의 번호, 안쪽 페이지 테이블의 번호, Offset으로 구성된다.

● Address-Translation Scheme
각각의 바깥쪽 페이지 테이블 Entry 한 개당 안쪽 페이지 테이블이 존재한다.
논리주소에서 바깥쪽 페이지 테이블의 Index를 가지고 p1번째 Entry를 가서 안쪽 페이지 테이블 중에 어떤 페이지 테이블인지 정보를 얻는다.
안쪽 페이지 테이블에서 물리적인 페이지 프레임 번호를 얻게 되며, 그 페이지 내에서 d만큼 떨어진 곳에서 원하는 정보를 찾을 수 있다.

안쪽 페이지 테이블은 테이블 자체가 페이지화 되어서 페이지 어딘가에 들어가 있게 된다.
2단계 페이지 테이블에서 기억해야 할 점은 안쪽 페이지 테이블의 크기가 페이지 크기랑 똑같다는 것이다.
보통 안쪽 페이지 테이블 하나의 크기는 페이지 테이블과 같은 4KB이다. Entry 하나의 크기가 4Byte, Entry는 1K 개.
32bit 주소 체계 중에서 Page Offset, p1, p2는 각각 몇 bit로 표현되어야 할까? Bit 수를 알기 위해서는 제일 안쪽에서부터 차례대로 올라가면 된다.
페이지 하나의 크기가 4KB(212Byte)이기 때문에 byte단위로 주소 구분을 하려면 12bit가 필요하다.
그래서 Page Offset은 12bit로 나타낸다.
이제 32bit에서 20bit를 나눠야 하며, 바깥쪽 페이지 테이블이랑 안쪽 페이지 테이블에서 주소 구분을 위해 bit를 정해줘야 한다.
안쪽 페이지 테이블에서 각 Entry 수가 1K 개가 있다. 서로 다른 210가지 Entry위치를 구분하기 위해서는 10bit가 필요하다.
그래서 안쪽 페이지 테이블의 크기가 10bit, 바깥쪽 테이블 10bit가 된다.
우리가 64bit 주소체계에서 페이지 크기는 똑같이 4KB, 2단계 페이지 테이블을 사용한다고 할 때, p1, p2 d는 몇 bit가 필요할지 생각해 보자.
